One of the composers continuing along the research path in microtonality, already laid down by Ligeti and perpetuated by Manfred Stahnke and Georg Hajdu, is also Canadian born Todd Harrop.
Since 2008, when he was introduced to Bohlen-Pierce (BP) tuning, he has been focused on exploring microtonal, non-octave scales by way of research and composition. Harrop has composed six works for various acoustic instruments able to play in this scale, e.g. “Calypso”, “Der Zauberzephir”, “Maelstrom” (two versions), “Bird of Janus”, plus a work-in-progress and has two more planned for the near future. Each piece is distinct not only in instrumentation but also in attempting to answer a research question related to some or several aspects of microtonality, e.g. can a scale without an octave adopt another interval as interval of equivalency – the perfect twelfth or perfect fifth, for instance. Inspired by his advisors Prof. Dr. Hajdu and Prof. Dr. Stahnke, Harrop has lately been combining two or more scales within the same piece and experimenting with ways of modulating, or ‘transferring’ (to borrow a term from Ivor Darreg) between them. His last performance/presentation was of a work-in-progress, “Apollo”, for percussion and computer, where the computer played in three scales based on dividing a perfect fifth into 8, 13 and 18 equal steps in order to be able to play a 6:7:9 septimal minor triad. This builds on techniques researched for an earlier work called “Bird of Janus”, where a solo clarinet alternates between scales in BP and Carlos Alpha, i.e. 13 steps per twelfth and 9 steps per fifth. In these and many other of Harrop’s works, we detect a clear road from a starting hypothesis, through its testing in an artistic context (often developing unique tools to help it’s realization), all the time documenting and being well-aware of the processes involved.
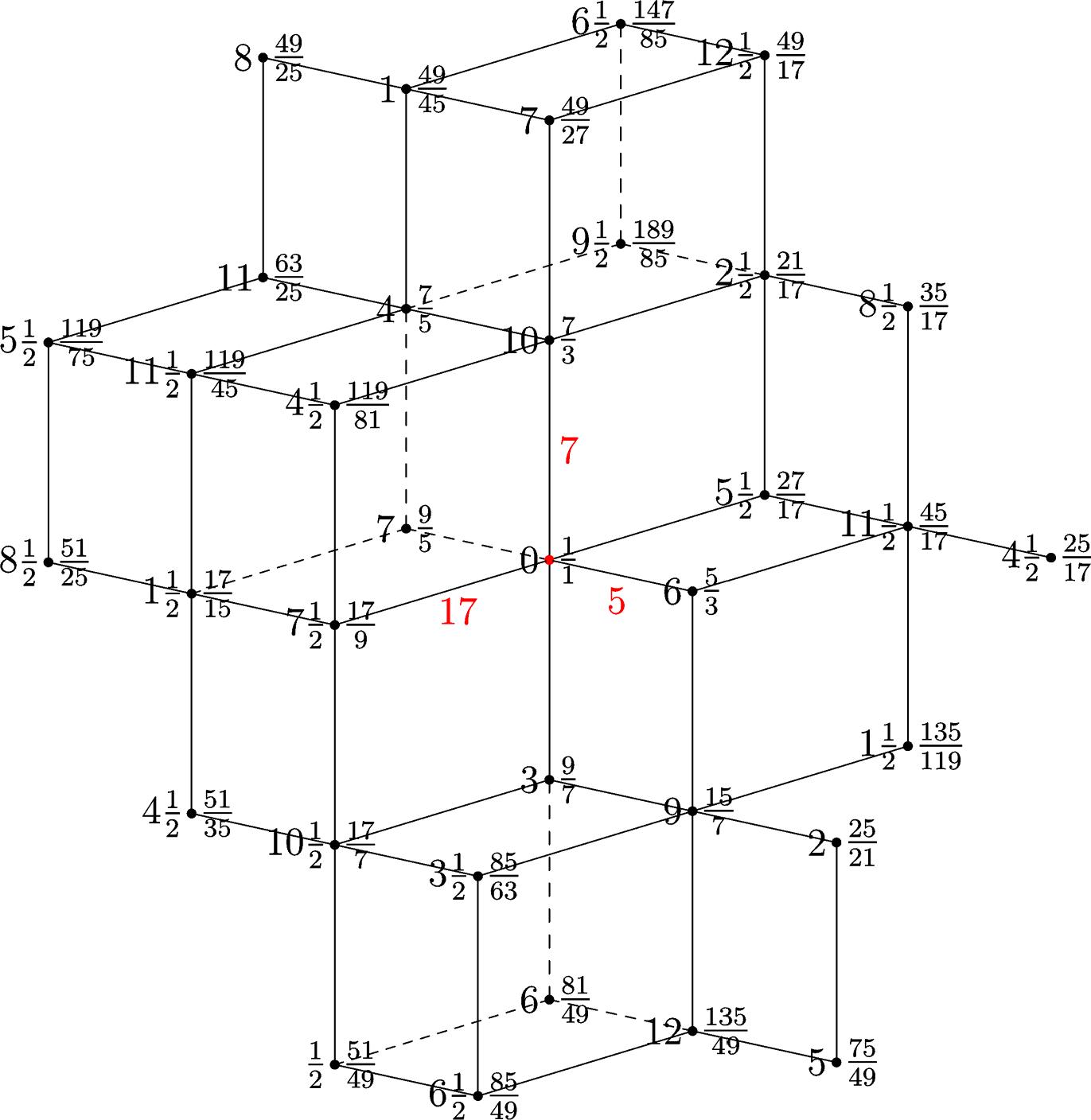
A 3-D lattice of a BP 1/2-tone scale[1]
[1] BP uses primes 3, 5 and 7 to express each scale step as a just intonation ratio, however, Todd’s lattice here introduces prime 17 in order to express scale steps halfway in between (more or less) the usual BP steps. Each axis represents prime number 5, 7 or 17, but prime 3 is flattened because it is implicit as an interval of equivalancy in BP theory – instead of 2/1 octave, inversions are at the 3/1 ‘tritave’ (twelfth).